「7」の倍数を表す正規表現の解説

オートマトンから正規表現への変換方法について、「7の倍数」を表す正規表現 - Qiitaをもとに書きます。

オートマトンとは？

状態(計算の途中結果)をもっていて、値が入力されると現在の状態と入力値をもとに次の状態へ遷移します。入力を受けるたびに「受理状態」「非受理状態」のどちらかになります。

ちょっと分かりづらいので、例をみていきいます。

7の倍数かを判定するオートマトン

たとえば「123456789」が7で割り切れるかは、筆算を使えば調べることができます。筆算はまず1桁みて7で割り、あまりを10倍して下の桁での計算に利用します。

 0 + 1 mod 7 -> 1
10 + 2 mod 7 -> 5
50 + 3 mod 7 -> 4
40 + 4 mod 7 -> 2
20 + 5 mod 7 -> 4

ここでいう「状態」は現在のあまりです(0 -> 1 -> 5 -> 4 -> 2 -> 4と遷移しています)。入力は各桁の数字です。状態が0の場合のみ受理します。

オートマトンの状態は以下のようになっています。

入力	現在の状態	次の状態
1	0	1
2	1	5
3	5	4
4	4	2
5	2	4
6	4	4
7	4	5
8	5	2
9	2	1

最終的な状態は1(123456789 mod 7 = 1)なので、非受理状態です。

なんとなく掴めてきたところで、いよいよオートマトンから正規表現を生成していきます。

7の倍数を判定するオートマトンの全容

10進法で考えると状態の遷移パターンが多くなってしまうので、ここでは2進法で考えます。2進数でも状態は余りの種類と同じ7つ用意すればいいです。遷移は次のとおりです。

遷移図

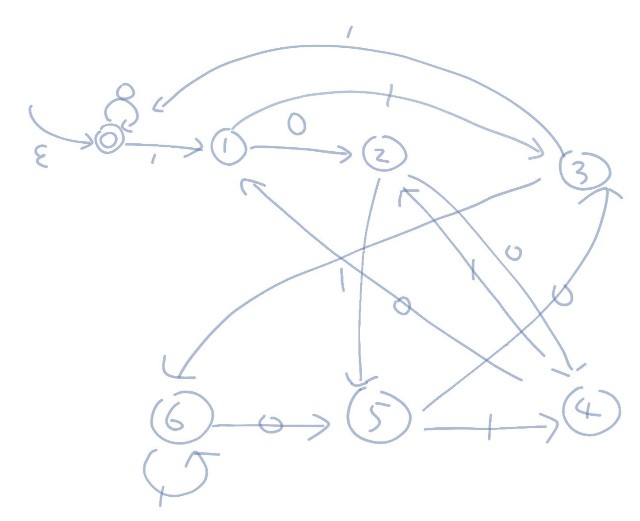
この図の各マスは状態を表しており、辺が遷移を表します。たとえば今の状態が1のときに1が入力されたら3へ遷移することが見るだけで分かるようになっています。

状態数を減らしていく

ここから状態を減らしていき、正規表現へ持ち込みます。まず、状態6に止まるべきだった入力はそもそも受け付けない(非受理とする)ことにして、状態6を削除します。すると、3 -> 6 -> 5という遷移が3 -> 5にまとめられます。

状態6を削除したあと

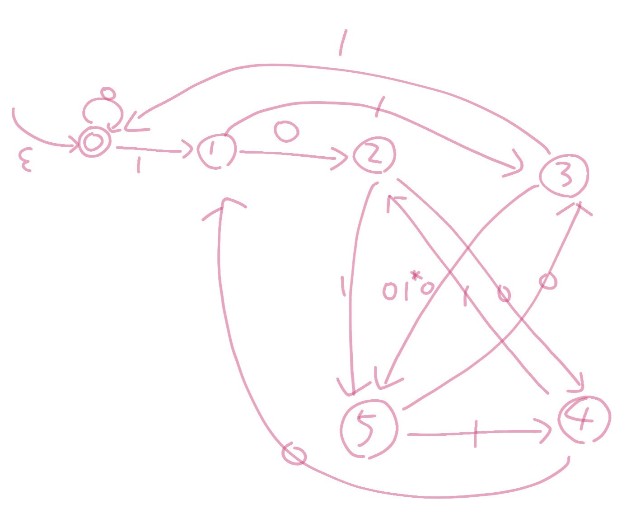
このように状態数を減らしていきます。ただ、この作業、恐ろしく面倒くさくて大変なので、状態数が2になった場面まで飛ばします。

状態数を2まで減らした遷移図

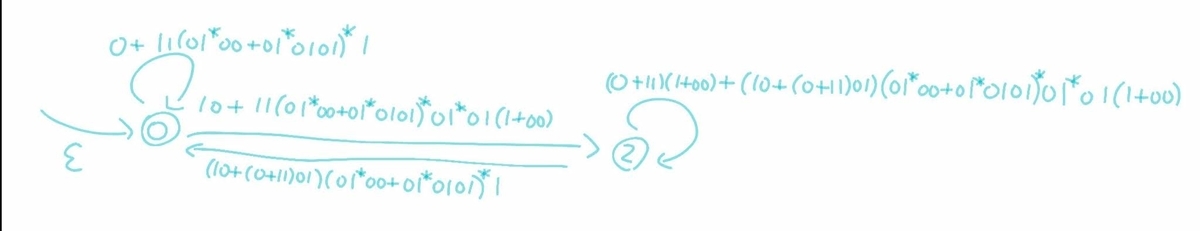
辺に書かれている正規表現が大変なことになっています。

最後に状態2も削除して、正規表現に落とし込んで完了です。

2進数で7の倍数を判定する正規表現

const reg = /^(11(01*00|01*0101)*1|0|(10|11(01*00|01*0101)*01*01(1|00))((0|11)(1|00)|(10|(0|11)01)(01*00|01*0101)*01*01(1|00))*(10|(0|11)01)(01*00|01*0101)*1)+$/;
console.log('検証スタート');
for (let i = 0; i < 1e6; ++i) {
    if ((i%7==0) !== reg.test(i.toString(2))) {
        throw new Error('正規表現で判定できていない数字が見つかりました');
    }
}
console.log('検証終了');

これで完成です。10⁶まで検証していますが、reg.test(n.toString(2))とn%7 == 0の結果が同じことがわかります。

7進法で7の倍数を判定する正規表現

2進数よりも遷移表が大きくなるぶん複雑になる…と思いきや、めちゃくちゃカンタンな正規表現で書けます。

/0$/ 以上です(当たり前)。

おまけ: 0000を受理しないようにする

実は上の正規表現では0000が受理されます。これを受理しないようにしてみます。

const reg = /^((11(01*00|01*0101)*1|(10|11(01*00|01*0101)*01*01(1|00))((0|11)(1|00)|(10|(0|11)01)(01*00|01*0101)*01*01(1|00))*(10|(0|11)01)(01*00|01*0101)*1)(11(01*00|01*0101)*1|0|(10|11(01*00|01*0101)*01*01(1|00))((0|11)(1|00)|(10|(0|11)01)(01*00|01*0101)*01*01(1|00))*(10|(0|11)01)(01*00|01*0101)*1)*|0)$/;

まあほぼ同じです。